Cet article présente de façon simplifiée un travail de recherche récent écrit en collaboration avec Grégory Châtel et Vincent Pilaud. Il a été publié dans la revue en ligne )i( interstices.
Ordres partiels
Tout le monde connaît l’ordre naturel des entiers : 1 est plus petit que 2 qui est plus petit que 3, etc. C’est ce qu’on appelle un ordre total. Les ordres partiels sont peut-être un peu moins familiers pour le grand public bien qu’on les retrouve dans de nombreux domaines (par exemple : l’ordre de dépendance des processus sur un ordinateur). Dans cet article, nous cherchons à mettre un ordre sur les ordres.
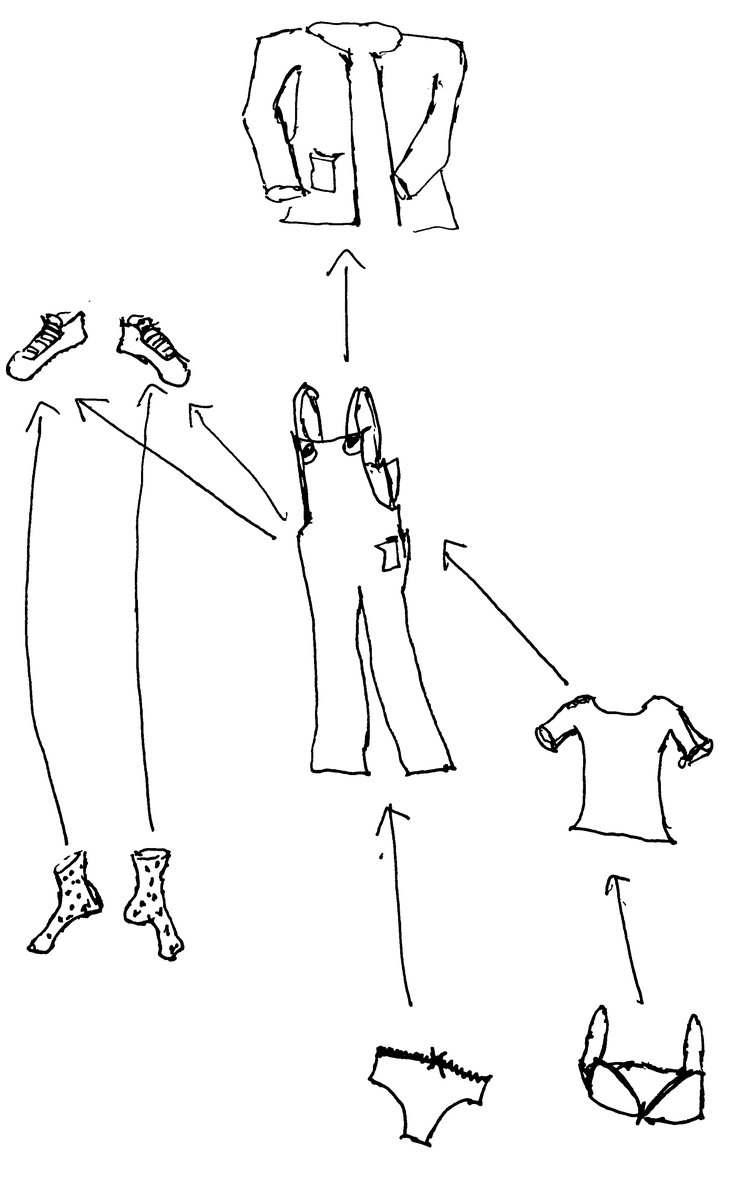
Tout d’abord, revenons sur la notion d’ordre partiel. Nous passons sur la définition formelle et donnons une idée plus intuitive : un ordre partiel est une façon d’ordonner les éléments d’un ensemble sans que chaque élément soit forcément comparable à tous les autres. Prenons un exemple concret et choisissons comme ensemble de départ les vêtements. On peut les ordonner selon l’ordre dans lequel il faut les enfiler : c’est un ordre partiel. En effet, on doit mettre son t-shirt avant sa salopette, mais l’ordre dans lequel on met ses chaussettes n’est pas important. On pourrait dire alors que le t-shirt est “plus petit” dans l’ordre partiel que la salopette mais que les chaussettes sont “incomparables” entre elles et incomparables au t-shirt. On le dessine de la façon suivante en mettant les éléments “plus petit” en bas et les “plus grand” en haut et en signifiant les dépendances avec des flèches.
Dans cet article, nous allons nous intéresser à la résolution d’une question logique sur un ordre partiel sur les relations binaires. Cette question est issue d’un article de recherche en informatique théorique, et plus précisément, en combinatoire. Vous trouverez ici l’article original The weak order on integer posets.
L’ensemble des relations binaires
Pour énoncer le problème, nous avons besoin de décrire les objets que nous allons ordonner. Jusqu’à présent, nous avons ordonné des nombres et des vêtements. Nous allons maintenant ordonner des graphes sur les entiers. Voici un exemple.
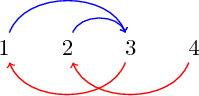
Nous avons ici un graphe orienté sur les entiers $1,2,3,4$. Pour plus de clarté, on a fait le choix de mettre en bleu et au dessus les arêtes qui vont de la gauche vers la droite (ici, $(1,3)$ et $(2,3)$) et en rouge en dessous celles qui vont de la droite vers la gauche (ici $(4,2)$ et $(3,1)$). On considère l’ensemble de ces graphes sans aucune restriction sur les arêtes.
Pourquoi étudions-nous ces graphes ?
Un autre mot que “graphes” pour décrire ces objets serait relations binaires. L’arête qui relie 1 à 3 signifie que 1 est en relation avec 3. Notez que la relation n’est pas symétrique : 2 est en relation avec 3 mais 3 n’est pas en relation avec 2. La notion de relation binaire est fondamentale en mathématique et en informatique théorique. C’est une structure de donnée que l’on retrouve dans de très nombreux contextes. Pensez par exemple à la structure d’un site web : on peut la voir comme une relation binaire entre les pages du site. Chaque page correspond à un numéro et l’on rajoute une arrête d’une page $A$ vers une page $B$ s’il existe un lien de $A$ vers $B$. Ici, notre motivation vient de la combinatoire algébrique qui cherche en particulier à traiter de problèmes issus des mathématiques fondamentales par des méthodes algorithmiques venues de l’informatique. Il se trouve que de nombreux objects combinatoires peuvent s’interpréter comme des relations binaires : par exemple les permutations et les arbres binaires.
Combien a-t-on de graphes possibles ?
C’est la première question que se pose un chercheur en combinatoire. Dans ce cas particulier, la réponse est relativement simple. Si on se limite aux graphes sur 1,2,3,4, il y a 3 arêtes possibles partant de 1 : $(1,2)$, $(1,3)$, et $(1,4)$. De même, il y a 3 arêtes possibles partant de 2, ainsi que de 3, ainsi que de 4 (Rappelez-vous que l’arête $(2,1)$ est différente de l’arête $(1,2)$). On a donc en tout $3 \times 4 = 12$ arêtes possibles. Chacune de ces arêtes peut soit être présente, soit absente, ce qui donne $2^{12} = 4096$ graphes possibles. De façon générale, on a $2^{n(n-1)}$ graphes possibles sur $1,2,\dots,n$.
Un ordre sur les graphes
Nous allons maintenant définir un ordre sur ces graphes, autrement dit : un ordre sur les relations binaires sur les entiers. Plus précisément, on va fixer un nombre $n$ qu’on appellera la taille du graphe, et on va décider d’un ordre partiel sur les $2^{n(n-1)}$ graphes possible sur $1,2,\dots,n$. Notez que le choix de cette définition est relativement arbitraire : elle est motivée par des considérations de recherche en combinatoire algébrique et nous verrons plus tard une interprétation plus intuitive. Nous avons choisi cette définition car elle nous a mené à des questions et des résultats intéressants.
Nous décidons que le plus petit graphe est celui qui contient le maximum d’arêtes bleues (d’un nombre plus petit vers un nombre plus grand) et aucune arête rouge (d’un nombre plus grand vers un nombre plus petit). Symétriquement, le graphe le plus grand est celui qui contient le maximum d’arêtes rouges et aucune arête bleue. Par exemple, pour la taille 4 :
| Graphe le plus petit | Graphe le plus grand |
|---|---|
 |
 |
On dira qu’un graphe $G$ est plus petit qu’un autre graphe $H$ si $G$ contient au moins les arêtes bleues de $H$ et si $H$ contient au moins les arêtes rouges de $G$ . Autrement dit : pour obtenir un graphe $H$ plus grand que $G$, je peux supprimer des arêtes bleues et rajouter des arêtes rouge. Par exemple :
| $G$ | $<$ | $H$ |
|---|---|---|
 |
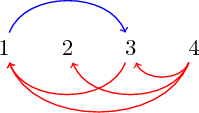 |
$G$ contient bien l’unique arête bleue de $H$ : $(1,3)$. Et $H$ contient les 2 arêtes rouges de $G$ : $(4,2)$ et $(3,1)$. C’est un ordre partiel car certains graphes ne sont pas comparable, par exemple
| $G$ | n’est pas comparable à | $H$ |
|---|---|---|
 |
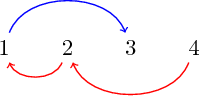 |
En effet, $G$ contient bien l’unique arête bleue de $H$, mais $H$ ne contient pas l’arête $(3,1)$ rouge de $G$. Voici par exemple une représentation de l’ordre partiel sur les 4 graphes de taille 2.
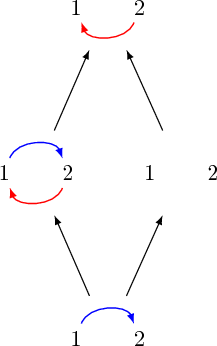
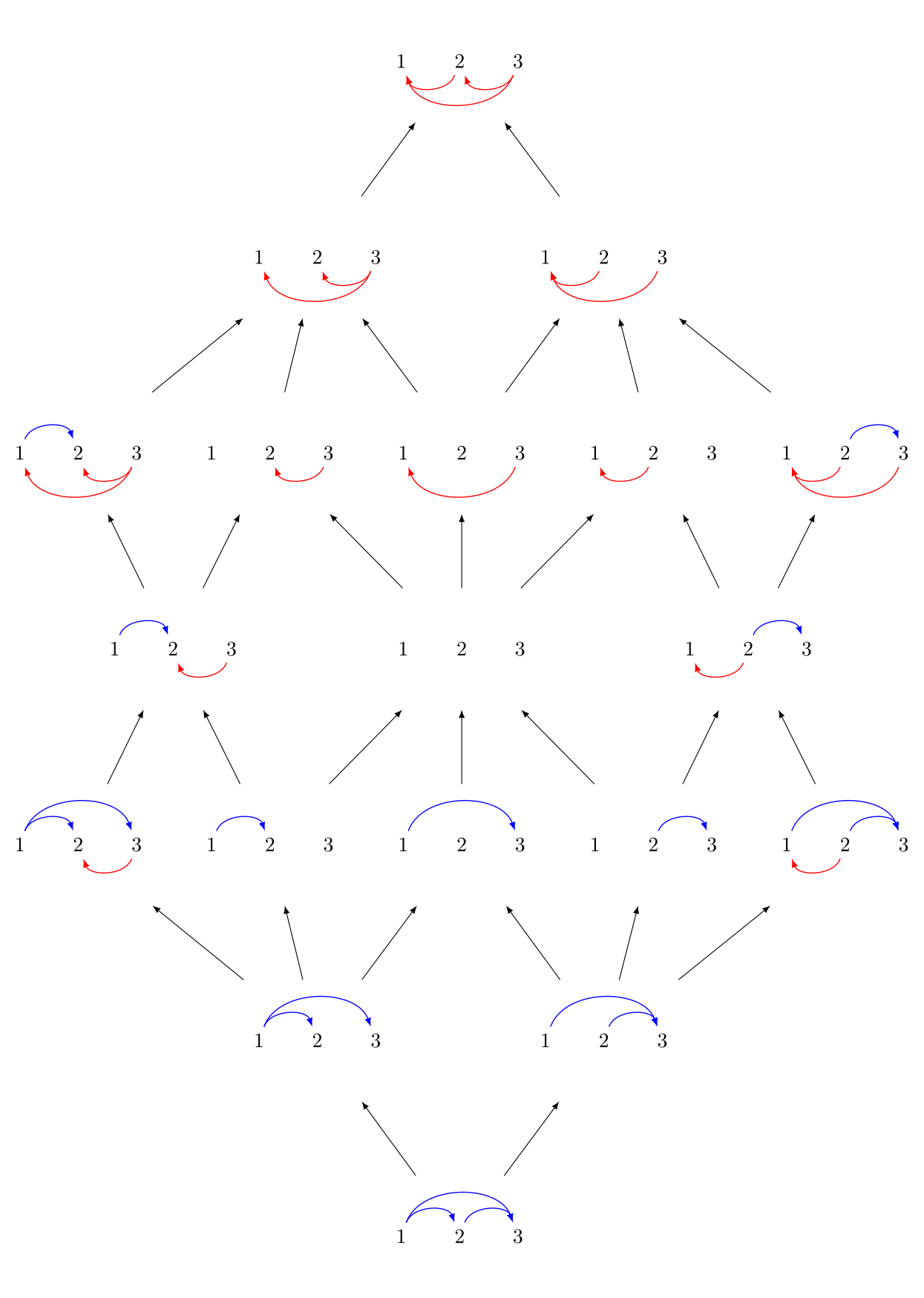
En taille 3, on a déjà 64 graphes et on obtient :
Des graphes qui sont des ordres
On a donc défini un ordre sur les graphes. À présent, nous allons voir que certains de ces graphes peuvent eux-mêmes être considérés comme des ordres partiels ! Observez le graphe suivant.

On dira qu’un nombre $a$ est plus petit dans le graphe qu’un nombre $b$ s’il existe une arête de $a$ vers $b$. On a par exemple que 1 est plus petit dans le graphe que 3 et 4, et que 5 est plus petit dans le graphe que 3. Certains nombres ne sont pas comparables car ils ne sont pas reliés par une arête : 1 et 2, 5 et 4, 1 et 5, etc. Le graphe définit donc un ordre partiel sur les nombre $1,2,3,4,5,6$. Notez qu’il y a donc 2 ordres distincts définis sur ces entiers : l’ordre naturel des nombres et l’ordre du graphe !
Tous les graphes définissent-ils un ordre partiel ? Voyons l’exemple suivant.

Ici, on aurait que 1 est plus petit dans le graphe que 3, lui même plus petit que 1. On dit que la relation n’est pas antisymétrique. Par ailleurs, 4 est plus petit que 2, qui lui est plus petit que 3. Mais il n’y a pas d’arête directe entre 4 et 3, donc 4 n’est pas plus petit dans le graphe que 3. On dit que la relation n’est pas transitive. Rappelons-nous l’ordre naturel des entiers et l’ordre des vêtements, on pourra vérifier qu’ils sont bien antisymétriques et transitifs. En effet, si l’ordre des vêtements n’était pas antisymétrique cela signifierait que je DOIS mettre un vêtement $A$ avant un vêtement $B$ et, en même temps, $B$ avant $A$ : j’obtiens une boucle et je ne peux plus m’habiller. La transitivité dit simplement que comme vous devez mettre votre t-shirt avant la salopette et la salopette avant les chaussures, alors vous devez mettre le t-shirt avant les chaussures pour pouvoir vous habiller. Ces deux propriétés suffisent à définir formellement une une relation d’ordre. On va donc sélectionner les graphes qui les vérifient.
| non antisymétrique | antisymétrique | antisymétrique |
|---|---|---|
| non transitif | non transitif | transitif |
 |
 |
 |
Des 64 graphes sur $1,2,3$, seulement 19 sont des relations d’ordres. On les ordonne entre elles en utilisant l’ordre sur les graphes et on obtient ce qu’on appelle l’ordre induit sur les relations d’ordre.
À quoi correspond cet ordre ? Que signifie-t-il ? On remarque la chose suivante : les relations bleues sont celles qui sont les mêmes que dans l’ordre naturel des entiers tandis que les relations rouges sont celles qui sont inversées. Ainsi le plus petit graphe est celui pour lequel 1 est plus petit que 2 qui est plus petit que 3 : c’est l’ordre naturel entre 1, 2 et 3. Dans le plus grand graphe, on a 3 plus petit que 2, plus petit que 1, soit le contraire de l’ordre classique. En clair, plus un graphe est petit dans notre ordre, plus il est proche de l’ordre naturel et plus il est grand, plus il est proche de l’ordre inverse.
Inf et Sup
Pour terminer, nous allons nous intéresser aux notions d’infimum et de suprémum. Observez l’ordre partiel sur les vêtements dessinés plus haut. Il y a sur le dessin exactement quatre vêtements que l’on doit mettre après la culotte ET le soutient-gorge : la salopette, la veste et les deux chaussures. Cet ensemble comporte un vêtement “minimum” que l’on doit mettre avant les trois autres : la salopette. C’est que qu’on appelle le supremum de la culotte et du soutient gorge car elle est à la fois “plus grande” que les deux mais aussi “plus petite” que tous les autres vêtements qui sont plus grands que les deux. La notion symétrique (le plus grand des plus petit) s’appelle l’infimum. Remarquez que le supremum et l’infimum n’existe pas toujours. Par exemple, imaginez quelqu’un qui refuse de mettre ses chaussures sans avoir mis ses deux chaussettes, on obtient l’ordre partiel suivant.
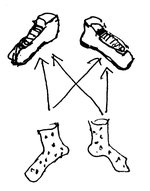
Ici, les deux chaussures sont supérieures aux deux chaussettes mais aucune n’est inférieure à l’autre : les chaussettes n’ont pas de suprémum.
Dans l’ordre partiel des relations binaires, si on oublie les contraintes d’antisymétrie et de transitivité, alors, tous les couples de graphes possèdent bien un suprémum et un infimum. Dans ce cas, on dit que l’ordre partiel est doté d’une structure de treillis. En effet, prenons deux graphes $G$ et $H$, le suprémum de $G$ et $H$ doit contenir toutes les arêtes rouges qui sont soit dans $G$, soit dans $H$, il doit donc contenir l’union des arêtes rouges. Par ailleurs, toutes ses arêtes bleues doivent être contenues à la fois dans $G$ et dans $H$, elles doivent donc appartenir l’intersection des arêtes rouges. Ainsi, le suprémum sera le graphe obtenu par l’union des arêtes rouges et l’intersection des arêtes bleues. Symétriquement, l’infimum sera obtenu par intersection des arêtes rouges et l’union des arêtes bleues. Voilà par exemple deux graphes avec leur infimum (en dessous) et supremum (au dessus).
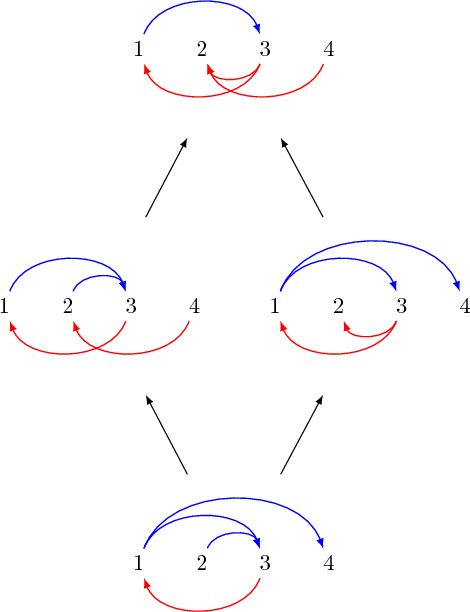
Mais que se passe-t-il si on rajoute les contraintes d’antisymétrie et de transitivité ? Avec seulement l’antisymétrie, il est encore assez simple de répondre. Observez par exemple les deux graphes antisymétriques ci-dessous avec leur infimum et supremum calculés comme nous l’avons expliqué : aussi bien l’infimum que le supremum sont eux aussi antisymétriques.

On peut prouver ce résultat de façon générale pour tout couple de graphes antisymétriques et nous invitons le lecteur à tenter cette petite démonstration ! On dit que l’ensemble des graphes antisymétriques forme un sous-treillis du treillis des graphes. Les choses se compliquent pour les relations transitives. Regardez l’exemple qui suit : les deux graphes de départ sont bien transitifs mais l’infimum et le supremum ne le sont pas (regardez par exemple 1-2-4 dans l’infimum et 2-1-3 dans le suprémum).

On peut tout de même prouver que l’ordre induit sur les relations d’ordre est aussi un treillis : il faut partir des infimum et supremum calculés comme ci-dessus et ajouter / supprimer les arêtes nécessaires. Nous laissons le lecteur sur ce problème et l’invitons à chercher la solution. Partez du treillis des 19 relations d’ordres que nous avons dessiné pour la taille 3 : arrivez-vous à trouver sur le dessin les infimum / supremum de deux graphes pris “au hasard” ? À partir de vos observations, pouvez-vous donner une méthode de calcul générique qui vous donne le résultat ? La réponse et la démonstration associée se trouvent dans l’article The weak order on integer posets avec de nombreux autres résultats que nous n’avons pas évoqués ici.
Note : les images (hors dessins) ont été obtenues grâce au logiciel mathématique libre sagemath.
Cet article et ses illustrations sont mis à disposition selon les termes de la Licence Creative Commons Attribution 4.0 International.