Les permutations sont des objets assez simples que l’on étudie parfois dès le lycée, mais savez-vous qu’elles sont aussi centrales dans de nombreux domaines de recherche en mathématiques discrètes et en informatique ? Dans cet article, nous présentons plusieurs interprétations de l’ensemble des permutations liées à la théorie des ordres, à l’algèbre et à la géométrie. Cet article est basé en partie sur mon travail de recherche et mon Habilitation à diriger des recherches.
Permutations
Imaginons que vous avez un paquet de 10 cartes, toutes différentes, combien de façons avez-vous de les ordonner ? C’est une question simple de dénombrement et la réponse consiste à compter les permutations. Les permutations d’un ensemble d’objets distincts sont simplement toutes les façons de “ranger” les éléments de cet ensemble. Prenons par exemple 3 cartes numérotées 1, 2, et 3. Vous pouvez faire 6 listes différentes
- 1,2,3
- 1,3,2
- 2,1,3
- 2,3,1
- 3,1,2
- 3,2,1.
Ce sont les 6 permutations d’un ensemble de taille 3. Le nombre de permutations se calcule facilement. Reprenons le cas des 10 cartes : pour la première carte, on a 10 possibilités, pour la seconde plus que 9, puis 8, etc. C’est-à-dire que pour chacune des 10 premières cartes, on a 9 possibilités pour la secondes ce qui signifie qu’on doit multiplier ces nombres et on obtient
\[10 \times 9 \times 8 \times 7 \times 6 \times 5 \times 4 \times 3 \times 2 \times 1 = 3628800.\]C’est qu’on appelle la fonction factorielle. De façon générale, on a
\[n! = n \times (n-1) \times \dots \times 1\]permutations d’un ensemble de taille $n$. Pour $n=3$, on trouve $3 \times 2 \times 1 = 6$ qui correspond bien à ce qu’on avait trouvé plus haut. Ce raisonnement est assez simple et peut être compris dès le collège. C’est souvent l’un des tous premiers exemples de dénombrement que l’on donne. Ce qui est moins connu c’est que les permutations sont en fait un objet actif de recherche présentes dans de nombreux domaines aussi variés que la bioinformatique, l’économie ou la théorie des représentations. Par exemple, la conférence internationale Permutation Patterns est organisée chaque année avec pour thème unique : les motifs dans les permutations. Dans cet article, nous expliquons certaines de leurs propriétés et comment elles créent le lien entre algèbre et géométrie.
Des sommets dans l’espace
Reprenons nos 6 permutations de tout à l’heure et interprétons les comme des points dans un espace à 3 dimensions. Par exemple, la permutation $2,1,3$ donne $x=2$, $y=1$ et $z=3$. Voilà ce que ça donne sur un cube :
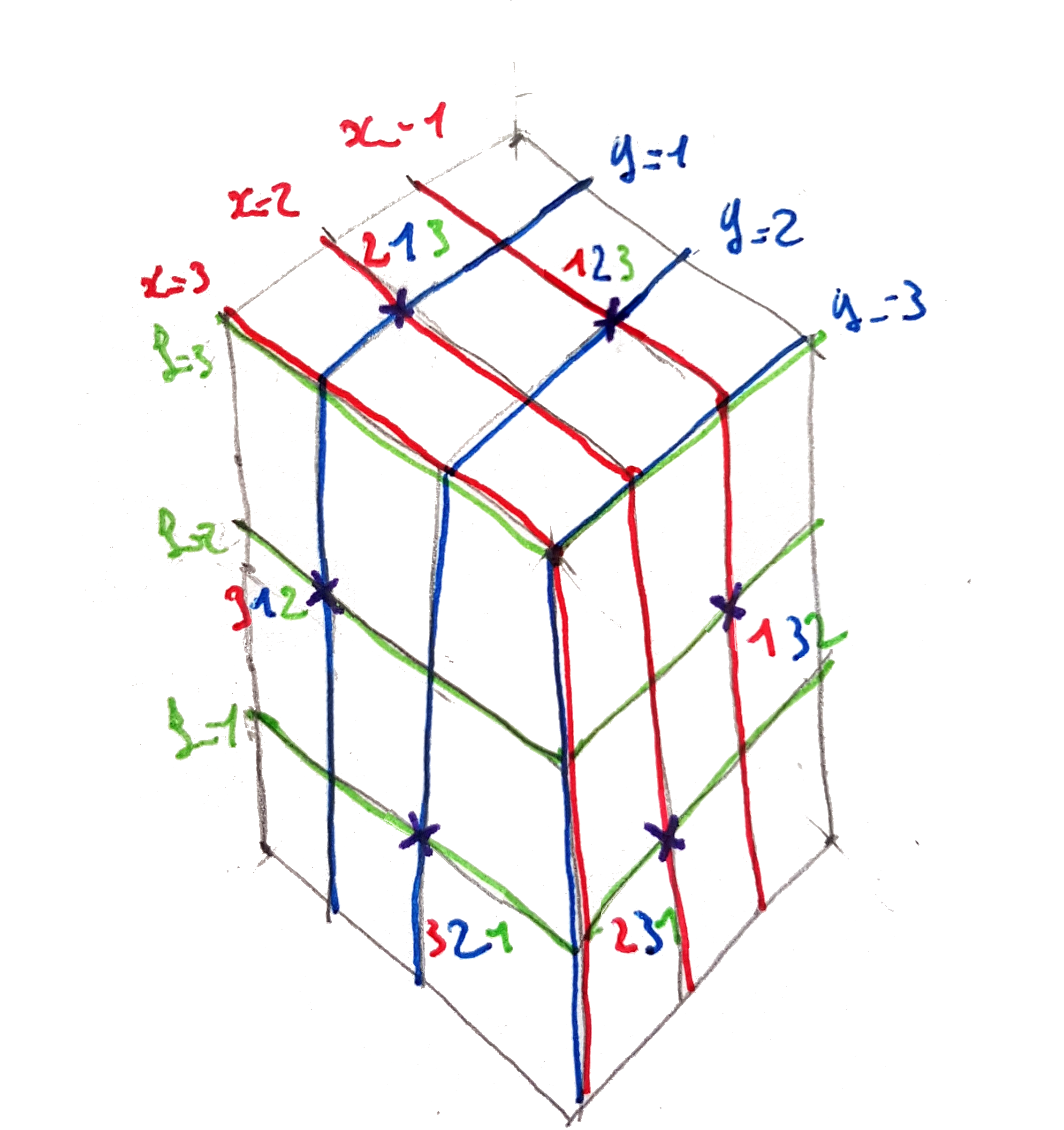
Comme la somme des coordonnées est toujours égales à 6, les 6 permutations appartiennent toutes à un même plan : on peut découper le cube de façon droite en touchant toutes les permutations. Par ailleurs, elles sont en position convexe, c’est-à-dire qu’elles semblent être “sur les bords”. Plus précisément, en prenant l’enveloppe convexe qui contient les 6 permutations, on obtient un hexagone dont les permutations forment les sommets (il n’y en a aucune à l’intérieur). Voici l’hexagone recréé de façon légèrement artisanale.

L’opération que nous venons de faire pour $n = 3$, placer les permutations dans un espace géométrique et prendre leur enveloppe convexe, est possible en augmentant la dimension $n$. L’objet obtenu est un polytope qu’on appelle le permutaèdre. Voilà le permutaèdre pour $n = 4$, qui est donc un polytope de dimension $3$.

On remarque de jolies propriétés que l’on retrouvera en dimension supérieure comme les nombreuses symétries ou le fait que les faces sont des hexagones et des carrés.
Mettons dans l’ordre
Dessinons à présent un graphe en mettant en relation les permutations reliées par une arête dans le permutaèdre. Pour les cas $n=3$ et $n=4$, on obtient
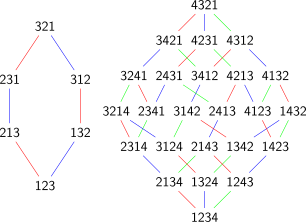
C’est une façon d’ordonner les permutations. Plus une permutation est “en bas”, plus les chiffres sont dans l’ordre. Les permutations sont regroupées par niveau, chaque niveau correspond au nombre de couples de chiffres dans le “désordre”. Ainsi suivre un chemin dans le graphe du haut vers le bas permet de définir un algorithme de tri. C’est en fait un algorithme connu et très peu efficace qu’on appelle habituellement le “tri à bulles”. Mais ce graphe a d’autres significations. Chaque arête échange deux chiffres de la permutation et la couleur indique quels chiffres sont échangés : les 2 premiers pour les arêtes rouge, les 2 du milieu pour les arêtes bleues et les 2 derniers pour les arêtes vertes. Voilà pour l’expliquation “simple” mais on peut aussi le dire en terme plus savant : on a dessiné le graphe de Cayley du groupe symétrique engendré par les transpositions simples. Le but ici n’est pas d’entrer dans les détails de chacune de ces définitions mais de voir que ce simple dessin fait le lien entre un objet combinatoire (les permutations), un objet géométrique (le permutaèdre) et un objet algébrique (le groupe symétrique ou groupe des permutations). C’est une des raisons qui font que le permutaèdre est un bel objet mathématique à l’origine de nombreux articles de recherche, généralisations, découvertes et curiosités dans différents domaines. Par exemple, un des premiers articles connus étudiant cet ordre sur les permutations est Analyse algébrique d’un scrutin publié par Guilbaud et Rosensthiel dans Mathématiques et Sciences Humaines en 1963. Les deux auteurs cherchaient alors à déterminer le meilleur résultat possible pour un vote donné où chacun ordonne ses candidats préférés.
Cet article et ses illustrations sont mis à disposition selon les termes de la Licence Creative Commons Attribution 4.0 International.